决策树 | 机器学习

发布 January 1, 2024 • 2 分钟 • 323 字

Table of contents

引言
概念
原理
决策树的流程
应用场景
代码实战
往期推荐

引言

机器学习领域中，决策树是一种强大的算法，被广泛应用于分类和回归问题。本文将深入探讨决策树的概念、原理、流程、工业应用场景，并通过代码实践展示其实现。

概念

决策树是一种树状模型，用于对实例进行决策。它的结构类似于流程图，其中每个内部节点代表一个特征或属性，每个分支代表一个决策，而每个叶子节点代表一个类别或输出。通过沿着树的分支进行决策，最终到达叶子节点以得到预测结果。针对“今天是否打高尔夫”这个问题决策树推理过程！

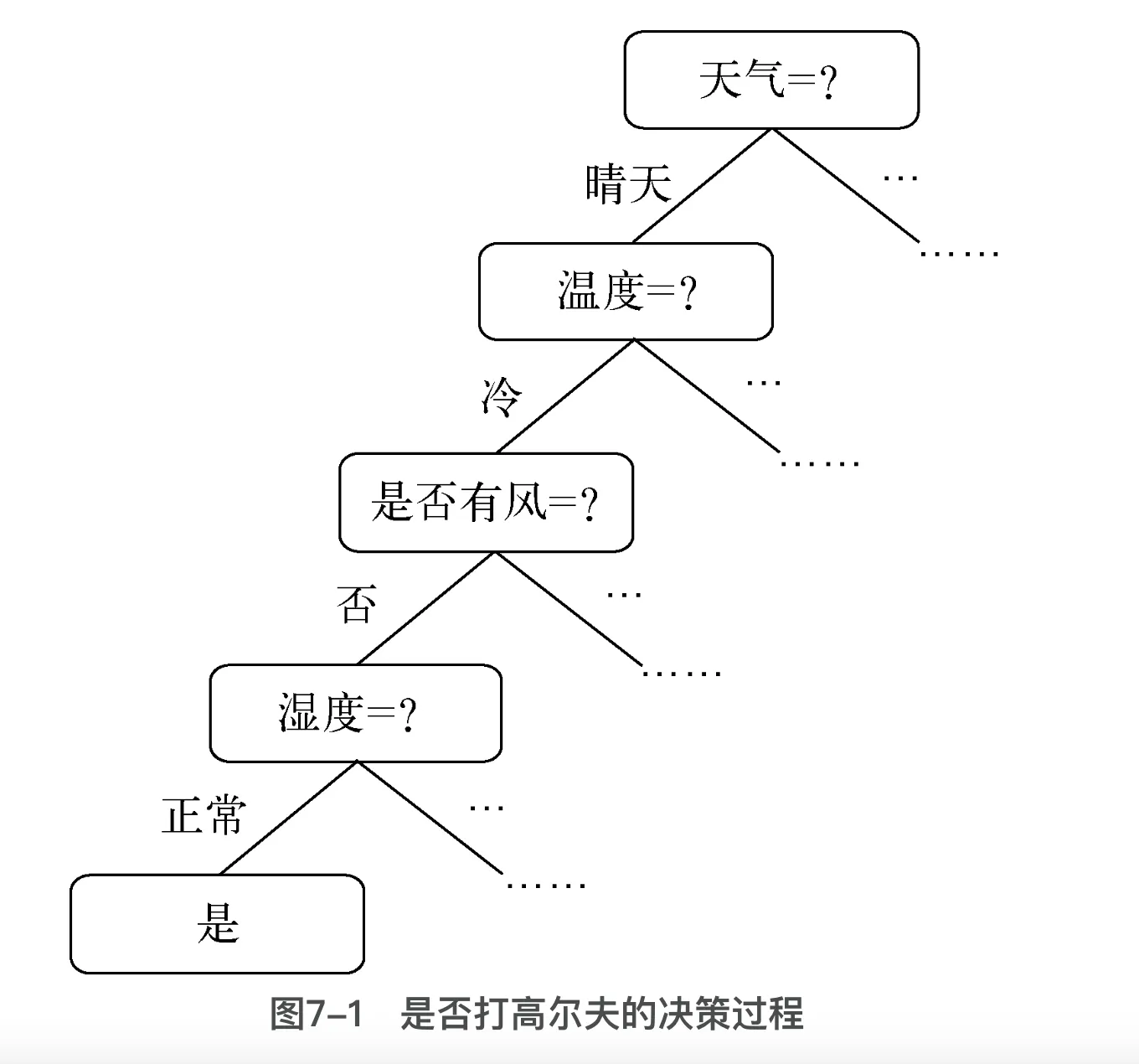
原理

决策树的构建基于信息论的概念。常用的决策树算法包括ID3、C4.5、CART等，它们通过选择最佳的特征进行节点分裂，以最大化信息增益或基尼指数。

决策树的组成

根节点（Root Node）： 决策树的起点，通常代表整个数据集。
内部节点（Internal Node）： 非叶节点，用于进一步划分数据。
叶节点（Leaf Node）： 决策树的终端节点，每个叶节点代表一个数据类别或预测值。

决策树的生成

特征选择

从训练数据中选出最佳特征作为当前节点的分裂标准。在决策树模型中，我们有三种方式来选取最优特征，包括信息增益、信息增益率和基尼指数。

信息增益

信息增益是一种用于特征选择的评估标准，它衡量了通过某一特征对数据进行划分后，数据纯度的提高程度。在决策树生成过程中，选择信息增益最大的特征作为当前节点的分裂标准。信息增益的计算公式为：

$$G(X, A) = H(X) - \sum_{i=1}^{m} \frac{|D_i|}{|D|} H(D_i)$$

其中：

$G(X, A)$ 是特征 $A$ 的信息增益；
$H(X)$ 是整个数据集的信息熵；
$D_i$ 是特征 $A$ 划分后的子数据集；
$|D_i|$ 是子数据集的大小；
$|D|$ 是整个数据集的大小；
$H(D_i)$ 是子数据集 $D_i$ 的信息熵。

信息增益越大，表示选择该特征进行分裂能够带来更大的纯度提升，使得决策更准确。

信息增益率

增益率是信息增益的一种变体，它对信息增益进行了归一化，解决了信息增益对取值数目较多的特征的偏好问题。增益率的计算公式为：

$$Gain_Ratio(X, A) = \frac{G(X, A)}{H(A)}$$

其中：

$ Gain_Ratio(X, A) $ 是特征 $ A $ 的增益率；
$ H(A) $ 是特征 $ A $ 的信息熵。

增益率不仅考虑了信息增益，还考虑了特征本身的信息熵，避免了对取值数目较多的特征的过度偏好。

基尼指数

基尼指数是衡量数据不纯度的指标，用于特征选择和节点分裂。在决策树中，选择基尼指数最小的特征进行分裂。基尼指数的计算公式为：

$$Gini(X) = 1 - \sum_{i=1}^{n} P(x_i)^2 $$

其中：

$ Gini(X) $ 是数据集 $X$ 的基尼指数；
$ P(x_i)$ 是第 $ i$ 个类别在总类别中的概率。

基尼指数越小，表示数据越纯净。选择基尼指数最小的特征进行分裂，能够使得决策树更加有效地进行分类。

综合而言，信息增益、增益率和基尼指数都在决策树中起到了关键的作用，帮助选择最佳的特征进行节点分裂，提高决策树的性能和泛化能力。

决策树的剪枝

预剪枝

在决策树生成过程中，对每个节点进行评估，若当前节点无法提高模型的泛化能力，则停止生成子节点。

后剪枝

先生成完整的决策树，然后从下到上对每个非叶节点进行评估，若删除或合并当前节点可以提高模型的泛化能力，则进行剪枝操作。

决策树的流程

数据准备： 收集并准备训练数据。
特征选择： 根据信息增益或基尼指数选择最佳的特征进行分裂。
节点分裂： 根据选定的特征将节点分裂成子节点。
递归构建： 对子节点递归执行上述步骤，直到满足停止条件。
剪枝： 避免过拟合，对决策树进行剪枝优化。

应用场景

决策树适用于简单而清晰的决策问题，具有易解释性和快速训练的特点，常见应用场景包括：

金融领域

信用评估：根据客户财务情况判断信用风险。
欺诈检测：识别可能的欺诈交易模式。

医疗领域

疾病分类：根据患者症状和检查结果辅助分类疾病。
治疗方案：根据患者特征推荐治疗方案。

制造业

质量控制：识别影响产品质量的关键因素。
生产优化：优化生产流程，提高效率。

营销和销售

客户分群：根据客户特征实现精准营销。
销售预测：预测不同产品销售情况，指导销售策略。

环境科学

生态系统评估：分析影响生态系统健康的因素。
自然灾害预测：通过观测数据预测自然灾害概率。

代码实战

# 导入必要的库
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
import matplotlib.pyplot as plt

# 加载信用卡欺诈检测数据集
url = "https://storage.googleapis.com/download.tensorflow.org/data/creditcard.csv"
df = pd.read_csv(url)

# 探索性数据分析
print(df.head())
print(df.info())
print(df['Class'].value_counts())

# 特征选择
X = df.drop('Class', axis=1)
y = df['Class']

# 数据集划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 数据标准化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

# 创建并训练逻辑回归模型
model = LogisticRegression()
model.fit(X_train, y_train)

# 在测试集上进行预测
y_pred = model.predict(X_test)

# 模型评估
print("Confusion Matrix:\n", confusion_matrix(y_test, y_pred))
print("\nClassification Report:\n", classification_report(y_test, y_pred))
print("\nAccuracy Score:", accuracy_score(y_test, y_pred))

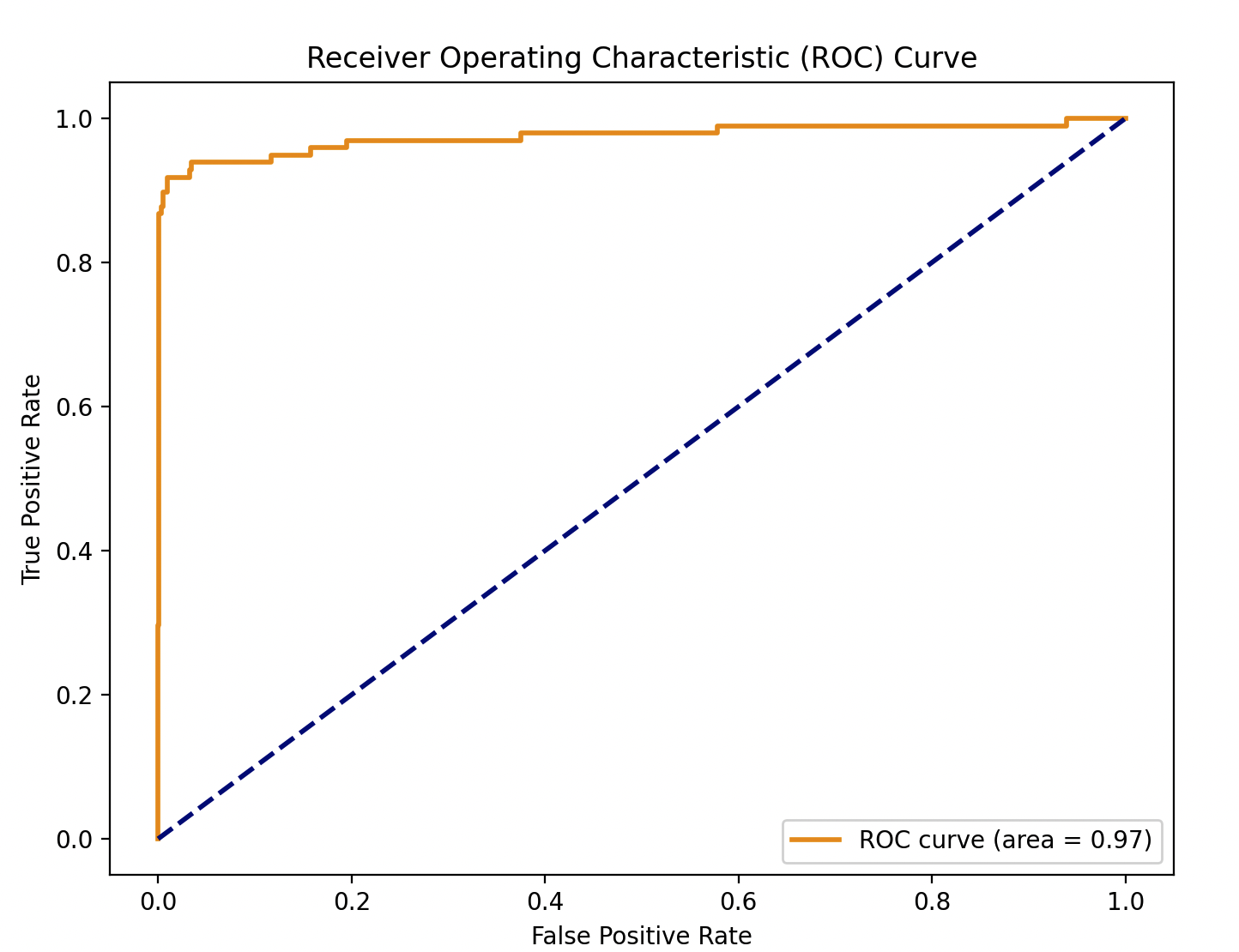
# 绘制ROC曲线
from sklearn.metrics import roc_curve, auc
fpr, tpr, thresholds = roc_curve(y_test, model.predict_proba(X_test)[:,1])
roc_auc = auc(fpr, tpr)

plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = {:.2f})'.format(roc_auc))
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC) Curve')
plt.legend(loc="lower right")
plt.show()

往期推荐

欢迎扫码关注公众号，订阅更多文章!

欢迎扫