支持向量机线性不可分 | 机器学习

发布 November 19, 2023 • 2 分钟 • 305 字

Table of contents

线性不可分 SVM
引入松弛变量
约束条件调整
超参数调整
实际应用
- 判断是否完全线性可分
- 决定是否引入参数 C
实战
- 数据加载预处理
往期推荐

本文从支持向量机线性不可分、软间隔、松弛变量、目标函数、约束条件、超参数 C,实际应用场景判别线性是否可分等几方面讲概述了支持向量机线性不可分

线性不可分 SVM

有些时候数据本身存在噪点或异常值、在这种场景下,支持向量机又会如何处理呢,看下图

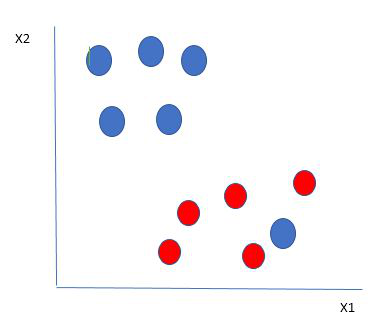
在这里，我们在红球的边界中有一个蓝球。那么 SVM 是如何对数据进行分类的呢？这很简单！红色球边界中的蓝色球是蓝色球的异常值。SVM 算法具有忽略异常值并找到使边际最大化的最佳超平面的特点。SVM 对异常值具有鲁棒性。

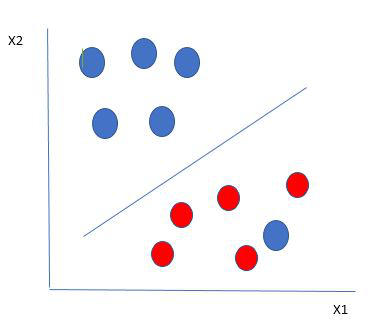
在这种类型的数据点中，SVM 所做的就是像之前的数据集一样找到最大边距，并在每次点跨越边距时添加惩罚。因此，此类情况下的边距称为软边距。当数据集存在软边距时，SVM 会尝试最小化(1/margin+∧(Σpenalty))。

引入松弛变量

首先，引入松弛变量（Slack Variables），这些变量表示数据点到超平面的距离。对于每个数据点，引入一个对应的松弛变量 $\xi_i$，表示第 $i$ 个数据点允许的错误。

目标函数修改 软间隔的目标函数通过调整传统硬间隔的目标函数，以考虑错误和松弛变量。新的目标函数可以表示为：

$ \min_{w, b, \xi} \frac{1}{2}||w||^2 + C \sum_{i=1}^{N} \xi_i $

其中：

$||w||^2$ 表示模型复杂度，即超平面的法向量的范数。 $\sum_{i=1}^{N} \xi_i$ 表示所有松弛变量的总和。 $C$ 是一个用户定义的超参数，用于平衡最小化模型复杂度和最小化分类错误的目标。

约束条件调整

随着引入了松弛变量，约束条件也需要相应的调整。约束条件现在变为：

$ y_i(w \cdot x_i + b) \geq 1 - \xi_i, \quad \text{for } i = 1, 2, \ldots, N $

这确保了即使数据点落在错误的一侧，它们的函数间隔仍然至少为 $1 - \xi_i$。

超参数调整

软间隔的效果受到超参数 $C$ 的影响， $C$ 的选择取决于对模型性能的需求。较大的 $C$ 值会更强调正确分类，但可能导致过拟合，而较小的 $C$ 值会更注重找到更大间隔，但可能容忍更多的错误分类。通过在实际问题中调整 $C$ 的值，可以根据具体情况平衡模型的复杂性和对错误的容忍度。这种灵活性使得软间隔成为处理线性不可分数据的有力工具。

实际应用

在实际数据集上应用软间隔 SVM 时，通常需要通过试验来确定最佳的超参数 $C$。这可能需要使用网格搜索或随机搜索等技术。软间隔 SVM 特别适用于那些数据本身就包含噪声或异常值的情况。它通过牺牲一些训练准确性，增加了模型对未见数据的泛化能力。

判断是否完全线性可分

可视化数据：如果数据维度较低（如二维或三维），可以通过可视化来初步判断数据是否可能线性可分。

尝试线性模型：在不考虑松弛变量的情况下，使用线性 SVM 或其他线性模型对数据进行拟合。如果模型表现良好，这可能表明数据是线性可分的。

评估模型性能：使用交叉验证等方法来评估线性模型的性能。如果线性模型的性能不佳，可能意味着数据不是完全线性可分的。

分析误差类型：查看模型的误差类型，如是否存在系统性误差，这可能表明数据结构的非线性特性。

决定是否引入参数 C

处理不完全线性可分的数据：如果数据不是完全线性可分的，引入 C 是必要的。这有助于控制模型对于误分类的惩罚强度。

防止过拟合：参数 C 可以帮助控制模型的复杂度，从而防止过拟合。特别是在数据量不是很大的情况下，合适的 C 值尤为重要。

模型调优：通过网格搜索、随机搜索或基于模型的搜索方法（如贝叶斯优化）来找到最优的 C 值。这通常是通过交叉验证完成的。

实验和验证：不同的 C 值可能会导致模型性能显著不同。实验不同的 C 值，并通过验证集或测试集来评估模型性能。

平衡偏差和方差：选择 C 值是平衡模型偏差和方差的一个重要步骤。较小的 C 值可能导致高偏差（欠拟合），而较大的 C 值可能导致高方差（过拟合）。

实战

数据加载预处理

# 导入所需的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import classification_report, confusion_matrix
import seaborn as sns

# 1. 数据加载
X, y = make_moons(n_samples=300, noise=0.2, random_state=42)

# 2. 特征工程 - 标准化处理
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 3. 探索性数据分析（EDA）
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.RdYlBu)
plt.title("EDA - Moon Dataset")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()

# 4. 模型训练和评估
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.3, random_state=42)

# 创建 SVM 模型
model = SVC(kernel='rbf', C=1, gamma=1)

# 训练模型
model.fit(X_train, y_train)

# 预测和评估
y_pred = model.predict(X_test)
print(classification_report(y_test, y_pred))

# 5. 参数调优 - 使用网格搜索
param_grid = {'C': [0.1, 1, 10, 100], 'gamma': [1, 0.1, 0.01, 0.001]}
grid = GridSearchCV(SVC(), param_grid, refit=True, verbose=2)
grid.fit(X_train, y_train)

# 输出最佳参数
print("Best Parameters:", grid.best_params_)

# 6. 可视化模型性能
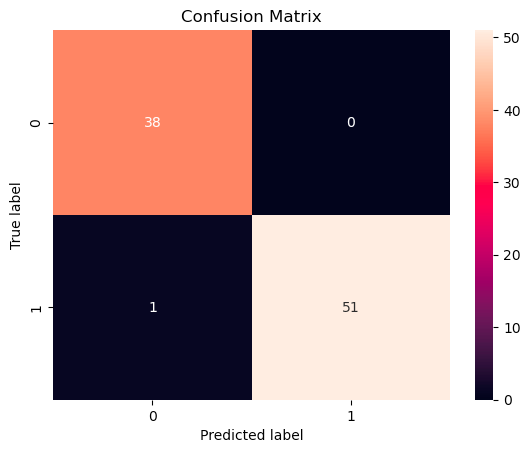
# 绘制混淆矩阵
cm = confusion_matrix(y_test, grid.predict(X_test))
sns.heatmap(cm, annot=True, fmt='g')
plt.title("Confusion Matrix")
plt.xlabel("Predicted label")
plt.ylabel("True label")
plt.show()

往期推荐

欢迎扫码关注公众号，订阅更多文章!

欢迎扫