Devean 布洛克
支持向量机线性可分 | 机器学习
November 18, 2023

支持向量机线性可分 | 机器学习

发布 November 18, 2023  •  2 分钟  • 316 字
Table of contents

本文从支持向量机概念、硬间隔、软间隔和非线性的区别、原理、术语、最大间隔数学推导几个方面详细讲解线性可分的支持向量机。

基础概念

支持向量机(Support Vector Machine)SVM，是一种监督学习模型，适用于二分类任务。SVM 算法的主要目标是在 N 维空间中找到能够将特征空间中不同类的数据点分开的最优超平面。超平面尝试使不同类的最近点之间的间隔尽可能最大。超平面的维度取决于特征的数量。如果输入特征的数量是两个，那么超平面只是一条线。如果输入特征的数量为三个，则超平面变为二维平面。当特征数量超过三个时就变得难以想象。

硬间隔、软间隔和非线性SVM区别

硬间隔

软间隔

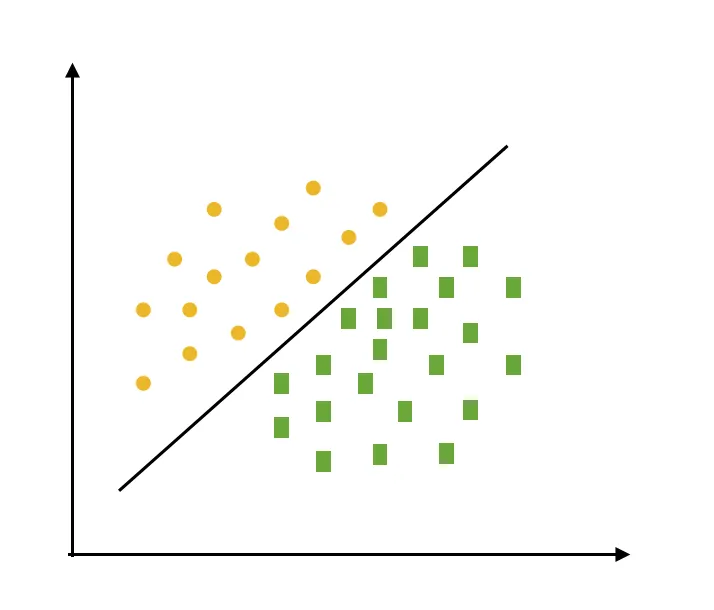
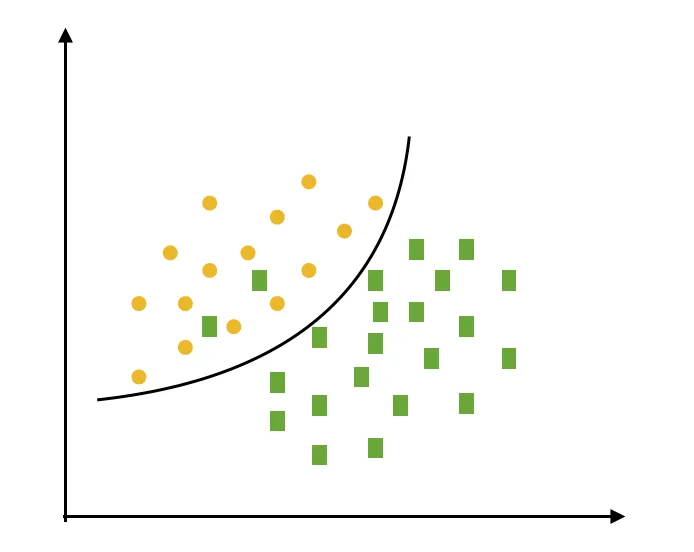
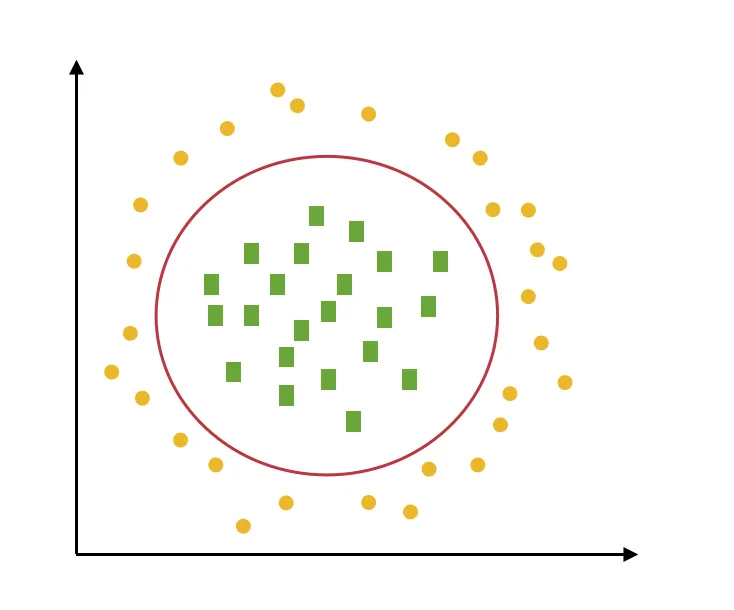
非线性可分

硬间隔数据是完全准确可分的、不存在分类错误的情况，软间隔是允许一定量的样本分类错误、而线性不可分是线性公式无解，只能使用非线性方式求解的

线性可分 SVM

即假设样本数据是线性可分离的情况下，我们直接使用线性 SVM 对数据进行分类。基本原理是找到一个超平面，将数据划分为两个类，使得类别之间的间隔最大化。

定义

给定训练样本集 D={(x1,y1)，(x2,y2)，…，(xm,ym)},yi∈{-1,+1}，分类学习最基本的想法就是基于训练集 D 在样本空间中找到一个划分超平面，将不同类别的样本分开。下面列子以二维数据展开、实际生活中多维数据与二维几乎无差别，只是数据特征维度变为了多维。

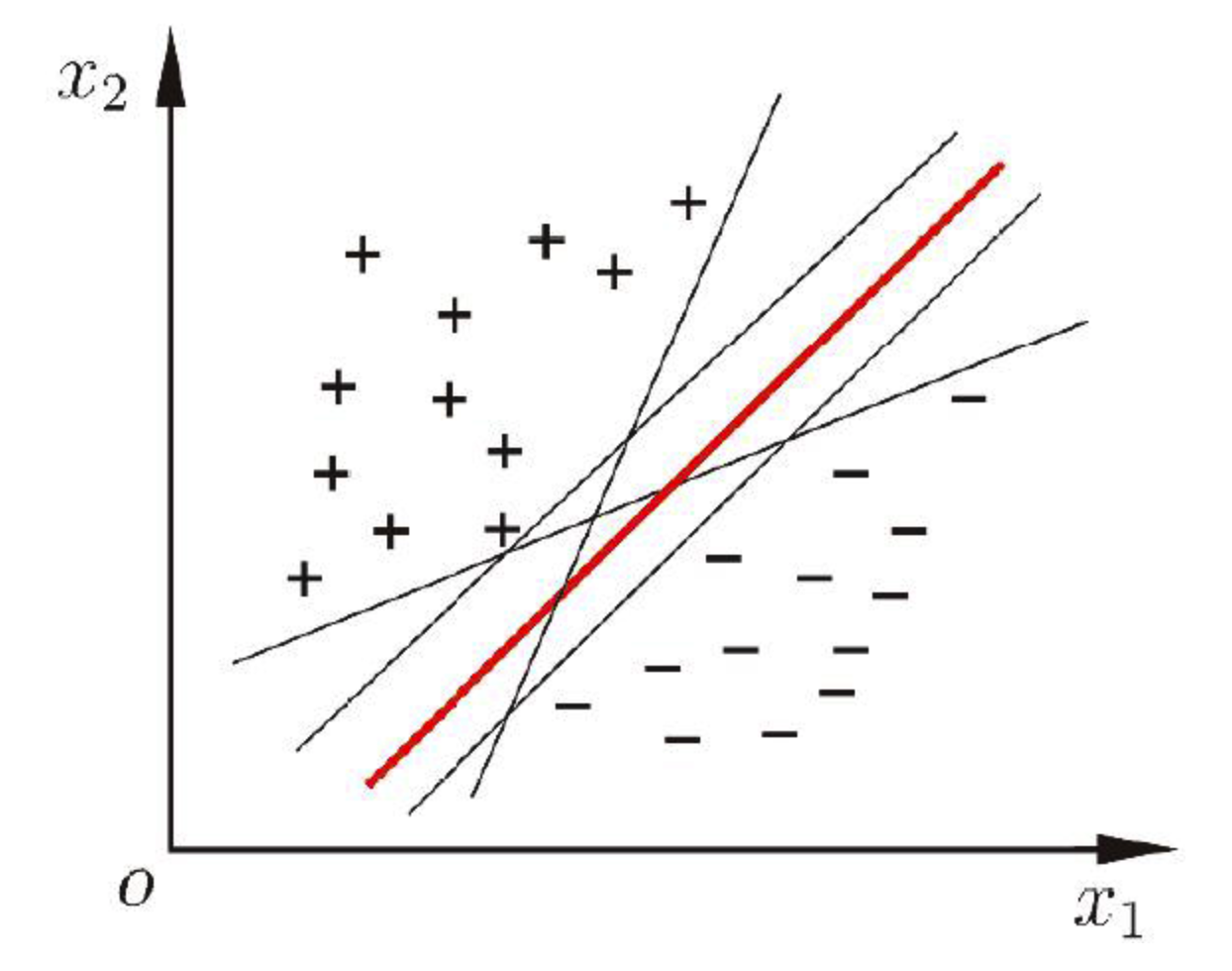
直观上看，应该去找位于两类训练样本“正中间”的划分超平面，即图中红色的那个，因为该划分超平面对训练样本局部扰动的“容忍”性最好。如果，由于训练集的局限性或噪声的因素，训练集外的样本可能比图中的训练样本更接近两个类的分隔界，这将使许多划分超平面出现错误，而红色的超平面受影响最小。

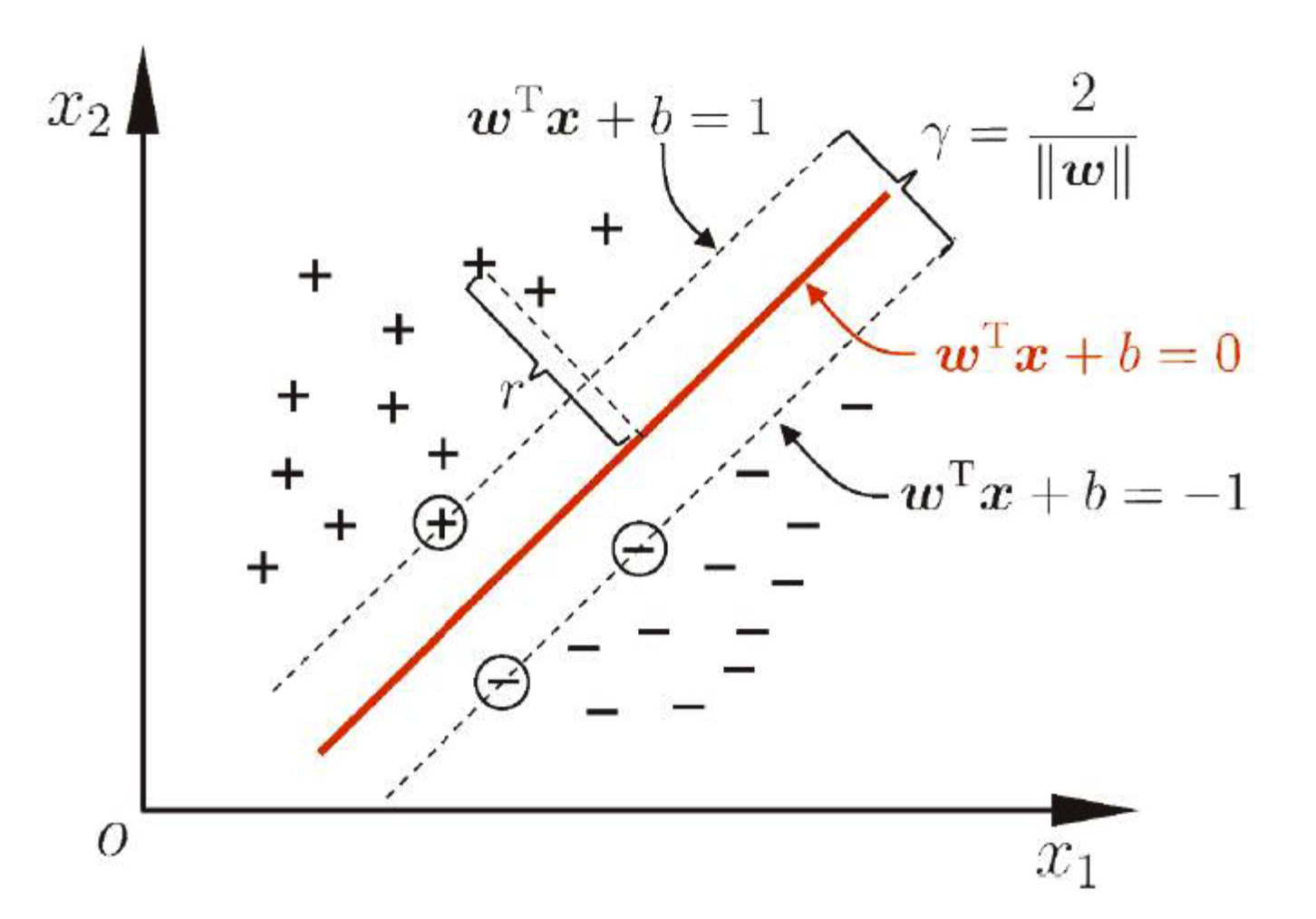
要找到最佳超平面,即得找到样本数据点离超平面最近的点的距离最大化，从上面两个图中可以看出,离图中红线最近的点即被圈住的样本到红色超平面距离最大。其中 w=(w1;w2;…;wd)为法向量，决定了超平面的方向；b 为位移项，决定了超平面与原点之间的距离。

术语

$$r= \frac {w^Tx+b} {||w||}$$

$$\lambda=\frac {2} {||w||}$$

求解线性 SVM 决策超平面

1. 列出知超平面方程组 $$w^Tx+b=0$$ $$w^Tx+b=1$$ $$w^Tx+b=-1$$
2 假设正负超平面向量 假设正决策超平面上的存在点 $x_m$、负决策超平面上存在点 $x_n$, 求两点之间的向量可如下图

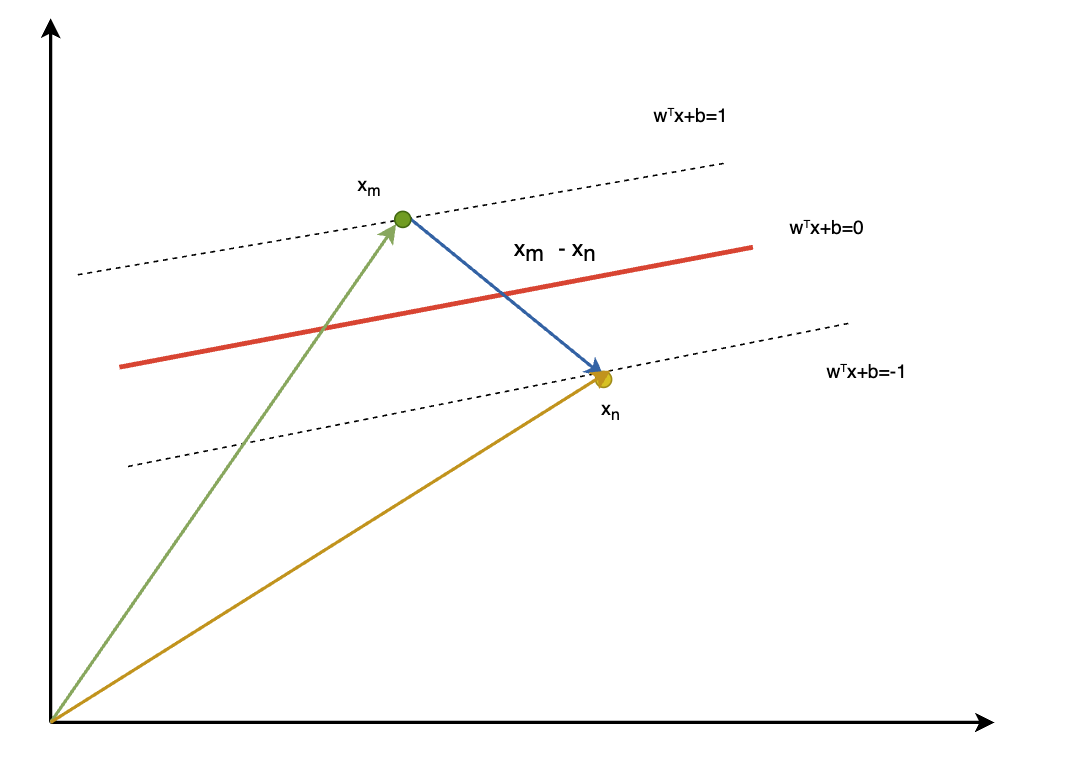
3.可将正负超平面上的向量带入方程计算

$$\vec w_m \vec x+b=1$$ $$\vec w_n \vec x+b=-1$$

$$\vec {w} \cdot (\vec x_m- \vec x_n)=2$$

4.在决策超平面上假设存在两点 $x_p,x_q$

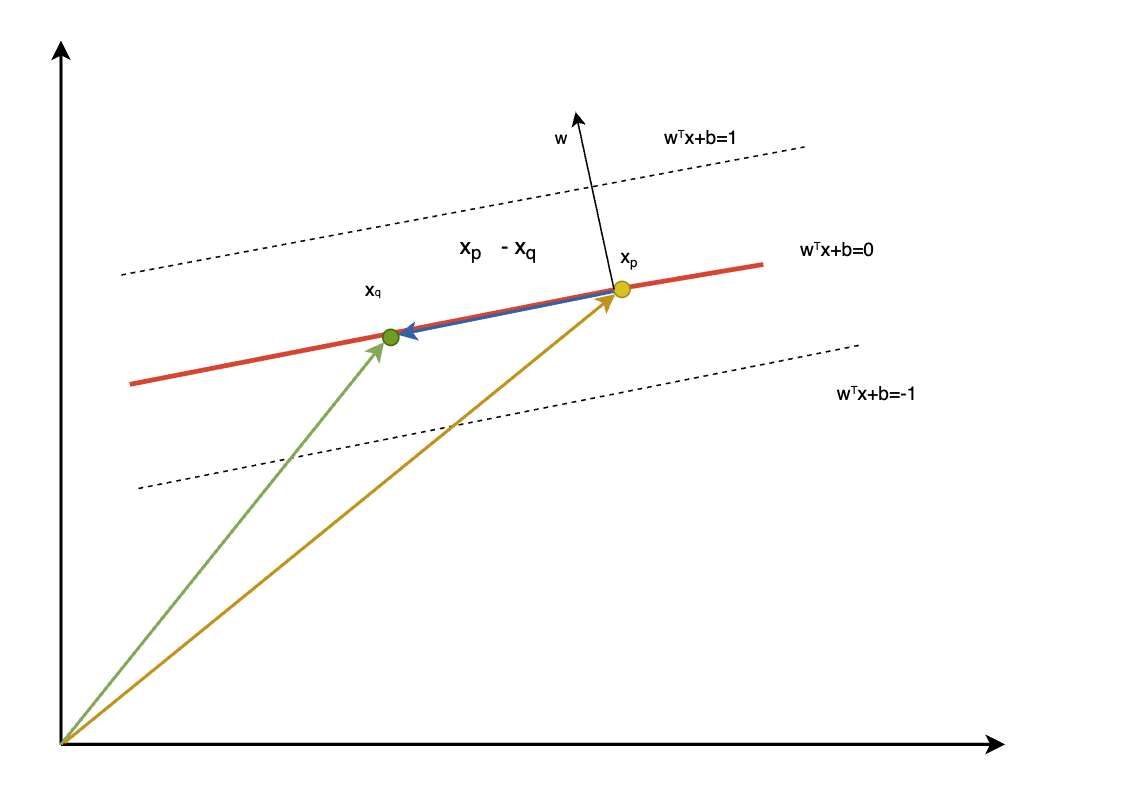
$$\vec w_p \vec x+b=0$$ $$\vec w_q \vec x+b=0$$

$$\vec {w} \cdot (\vec x_p- \vec x_q)=0$$

5. 由此 我们可推出向量 $\vec w$ 与超平面垂直，即为超平面的法向量

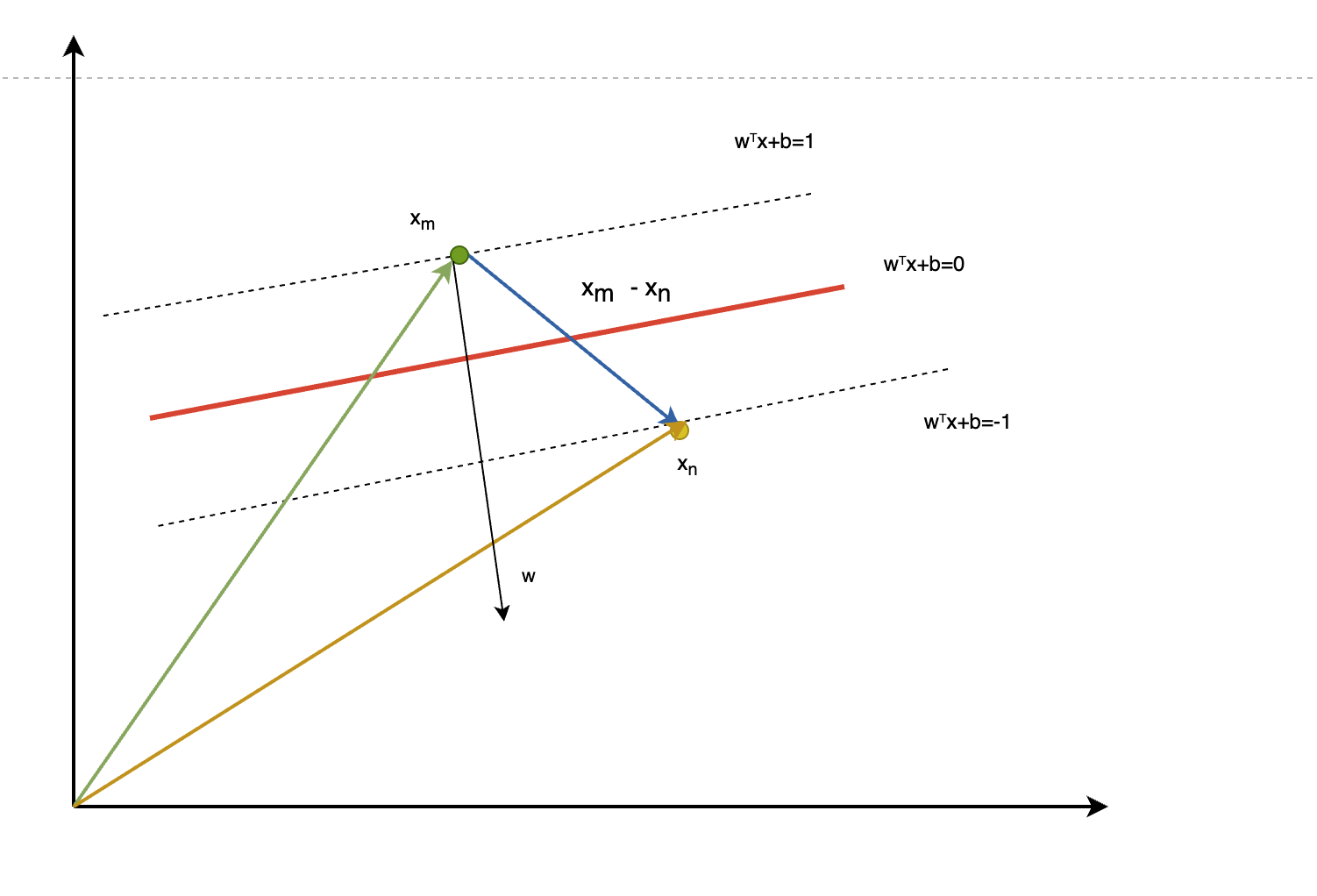
6.基于向量定理计算 根据已知,及上图结论，我们可推导出 $$\vec {w} \cdot (\vec x_m- \vec x_n)=2$$ $$||\vec x_m- \vec x_n|| * cos \theta * ||\vec {w} || =2$$

7. 推导间隔 L 从上图中可以看出向量 $\vec x_m- \vec x_n$ 投影到法向量 $\vec w$ 上，就等于间隔 L

$$||\vec x_m- \vec x_n|| * cos \theta =L$$

$$L * ||\vec {w} || =2$$

$$L = \frac {2} {||\vec {w} ||}$$

8.定义问题 我们的目标是最大化分类间隔，即最大化 $\frac{2}{|w|}$。等价地，我们最小化 $\frac{1}{2} |w|^2$。优化问题可以写成：

最小化:

$$ \frac{1}{2} |w|^2 $$

约束条件:

$$ y_i(w \cdot x_i + b) \geq 1 \quad \text{for all } i = 1, 2, \ldots, m $$

9. 引入拉格朗日乘子：

引入拉格朗日乘子 $\alpha_i \geq 0$，定义拉格朗日函数：

拉格朗日方程:

$$ L(w, b, \alpha) = \frac{1}{2} |w|^2 - \sum_{i=1}^{m} \alpha_i [y_i(w \cdot x_i + b) - 1] $$

10. 求解对偶问题：

通过对拉格朗日函数对 $w$ 和 $b$ 求偏导数，并令其等于零，我们得到：

偏导数与置换:

$$ w = \sum_{i=1}^{m} \alpha_i y_i x_i $$

对偶问题:

$$ \text{maximize} \quad W(\alpha) = \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i,j=1}^{m} \alpha_i \alpha_j y_i y_j x_i \cdot x_j $$

$$ \text{subject to} \quad \alpha_i \geq 0, \quad \sum_{i=1}^{m} \alpha_i y_i = 0 $$

11. 最大化间隔的数学表达：

通过对偶问题的求解，得到一组优化的拉格朗日乘子 $\alpha^*$。最大化分类间隔的数学表达式为：

最大间隔:

$$ \text{maximize} \quad \frac{2}{|w|} = \frac{2}{\sqrt{\sum_{i=1}^{m} (\alpha_i^* y_i x_i)^2}} $$

12. 计算最大间隔：

最大间隔的计算是通过对偶问题中的 $ \alpha^* $ 计算得到的。具体地，最大间隔是 $ \frac{2}{|w|} $，其中 $w$ 由 $ \sum_{i=1}^{m} \alpha_i^* y_i x_i $ 计算得到。

欢迎大家关注

往期推荐