非线性支持向量机 |机器学习

发布 December 2, 2023 • 3 分钟 • 507 字

Table of contents

核心概念
- 线性与非线性 SVM
核技巧（Kernel Trick）
目标函数引入核函数
构建决策函数
应用实例
总结
非线性 SVM 的优势与局限性
往期推荐

非线性支持向量机（SVM）是一种强大的监督学习算法，用于解决分类和回归问题。它通过使用核技巧将数据映射到高维空间，从而处理非线性关系。在这篇文章中，我们将探讨非线性 SVM 的工作原理、核函数的作用以及如何在实际中应用非线性 SVM。

核心概念

线性与非线性 SVM

线性 SVM 在处理线性可分数据时效果显著。然而，当数据集呈非线性分布时，线性 SVM 的性能会受限。非线性 SVM 通过核技巧解决了这个问题。

核技巧（Kernel Trick）

什么是核技巧？

核技巧是一种通过转换将低维输入空间映射到高维特征空间的方法，它使得非线性特征组合可以被 SVM 以线性方式处理，核技巧由一些数学工具核函数实现。

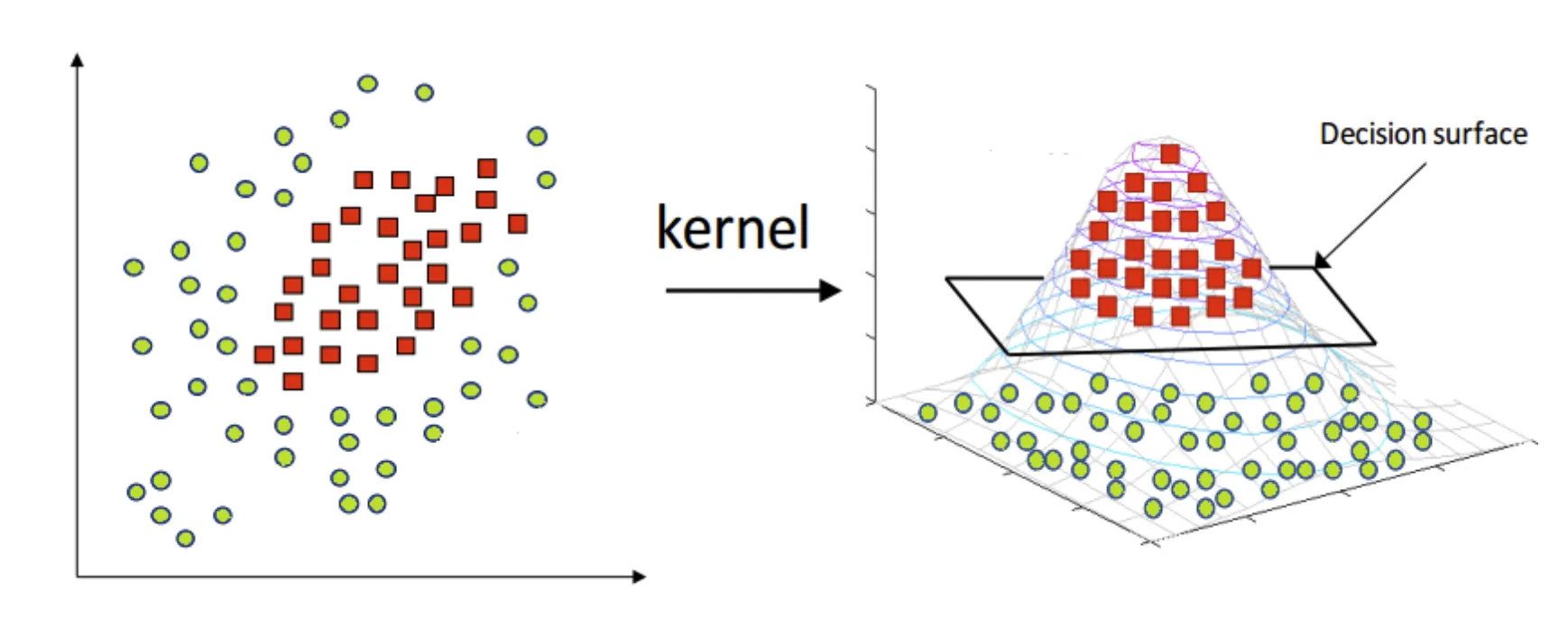
核函数定义

核函数是一个数学函数，能够计算数据点在高维特征空间中的内积，而无需直接计算这些特征。换句话说，它可以让我们在原始特征空间中间接地计算在更高维特征空间的内积。

核函数的作用

维度映射： 核函数通过隐式地将数据映射到一个更高维的空间，帮助处理数据的非线性特征。
计算简化： 直接在高维空间中处理数据是复杂和计算密集的。核函数通过在原始空间中进行计算来避免这个问题，从而简化了计算过程。
处理非线性问题： 在许多实际问题中，数据集无法用线性方法分割。核函数使 SVM 能够通过在高维空间中寻找线性边界来处理这些非线性问题。

常见的核函数

高斯径向基函数（RBF）核： 最常用的核函数，适合处理没有明显特征模式的复杂数据集。 $$K(\mathbf{x}_i, \mathbf{x}_j) = \exp(-\gamma ||\mathbf{x}_i - \mathbf{x}_j||^2)$$ 其中，$\gamma$ 是缩放参数。

多项式核： 用于将数据映射到由原始特征的多项式组成的高维空间。 $$K(\mathbf{x}_i, \mathbf{x}_j) = (\gamma \mathbf{x}_i \cdot \mathbf{x}_j + r)^d$$

其中，$\gamma$ 是缩放参数，$d$ 是多项式的度数,$ r $ 是系数项。

Sigmoid 核： 类似于神经网络的激活函数。

$$K(\mathbf{x}_i, \mathbf{x}_j) = anh(\gamma \mathbf{x}_i \cdot \mathbf{x}_j + r)$$ 其中，$\gamma$ 是缩放参数，$r$ 是偏置项。

目标函数引入核函数

对于非线性数据集，目标函数和约束条件与线性不可分 SVM 类似，但使用核技巧在高维空间中寻找最优超平面。

目标函数:

$\max_{\alpha} \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i,j=1}^n y_i y_j \alpha_i \alpha_j K(\mathbf{x}_i, \mathbf{x}_j)$
约束条件调整:

$\sum_{i=1}^n y_i \alpha_i = 0 \text{ and } 0 \leq \alpha_i \leq C, \quad \forall i$

构建决策函数

在找到最优超平面后，SVM 使用决策函数来评估新样本属于哪个类别。 $$ f(x)=sign(∑_{i=1}^ny_iα_iK(x_i,x)+b) $$

应用实例

支持向量机用于预测股票价格（例如标普 500ETF，代码为 ‘SPY’）的未来 ’n’ 天收盘价的机器学习模型。


# 基础库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties

plt.style.use('fivethirtyeight')
# 设置中文字体
fontPath = '/System/Library/Fonts/PingFang.ttc'
myFont = FontProperties(fname=fontPath)

# 预处理
from sklearn.preprocessing import MinMaxScaler
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split, TimeSeriesSplit, GridSearchCV

# SVM
from sklearn.svm import SVR

# 忽略警告
import warnings

warnings.filterwarnings('ignore')

# 使用 yfinance 加载数据
import yfinance as yf

# 创建变量来预测 'n' 天之后的价格
n = 5

# 从 yfinance 加载 SPY 的数据
df = yf.download('SPY', start='2020-01-01', end='2023-12-02', progress=False)
df = df[['Adj Close']]

# 打印数据的最后 5 行
print(df.tail())

# 创建目标变量
df['Target'] = df['Adj Close'].shift(-n)
print(df.tail(6))

# 构建预测变量和目标变量
X = df[['Adj Close']].values[:-n]
y = df['Target'].values[:-n]

# 拆分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0, shuffle=False)

# 打印训练集和测试集的大小
print(f"训练集和测试集大小：{len(X_train)}, {len(X_test)}")

# 使用管道进行特征缩放和模型训练
pipe = Pipeline([("scaler", MinMaxScaler()), ("regressor", SVR(kernel='rbf', C=1e3, gamma=0.1))])
pipe.fit(X_train, y_train)

# 预测测试集
y_pred = pipe.predict(X_test)

# 输出模型得分
print(f'训练集准确率：{pipe.score(X_train, y_train):0.4f}')
print(f'测试集准确率：{pipe.score(X_test, y_test):0.4f}')

# 使用时间序列交叉验证
tscv = TimeSeriesSplit(n_splits=5)

# 获取参数列表
pipe.get_params()

# 网格搜索和拟合模型
param_grid = {
    "regressor__C": [0.1, 1, 10, 100, 1000],
    "regressor__kernel": ["poly", "rbf", "sigmoid"],
    "regressor__gamma": [1e-7, 1e-4, 1e-3, 1e-2]
}

gs = GridSearchCV(pipe, param_grid, n_jobs=-1, cv=tscv, verbose=1)
gs.fit(X_train, y_train)

# 输出最佳模型得分
print(f'训练集准确率：{gs.score(X_train, y_train):0.6f}')
print(f'测试集准确率：{gs.score(X_test, y_test):0.6f}')

# 创建 DataFrame 来包含关键值
df3 = pd.DataFrame({'X': X_test.flatten(), 'y': y_pred})
df3['X'] = df3['X'].shift(-n)
df3['X-y'] = df3['X'] - df3['y']
df3 = df3[:-n]

# 检查缺失值
df3.isnull().sum()

# 输出均值差异
print(f'均值差异：{np.mean(df3["X-y"]):0.4f}')

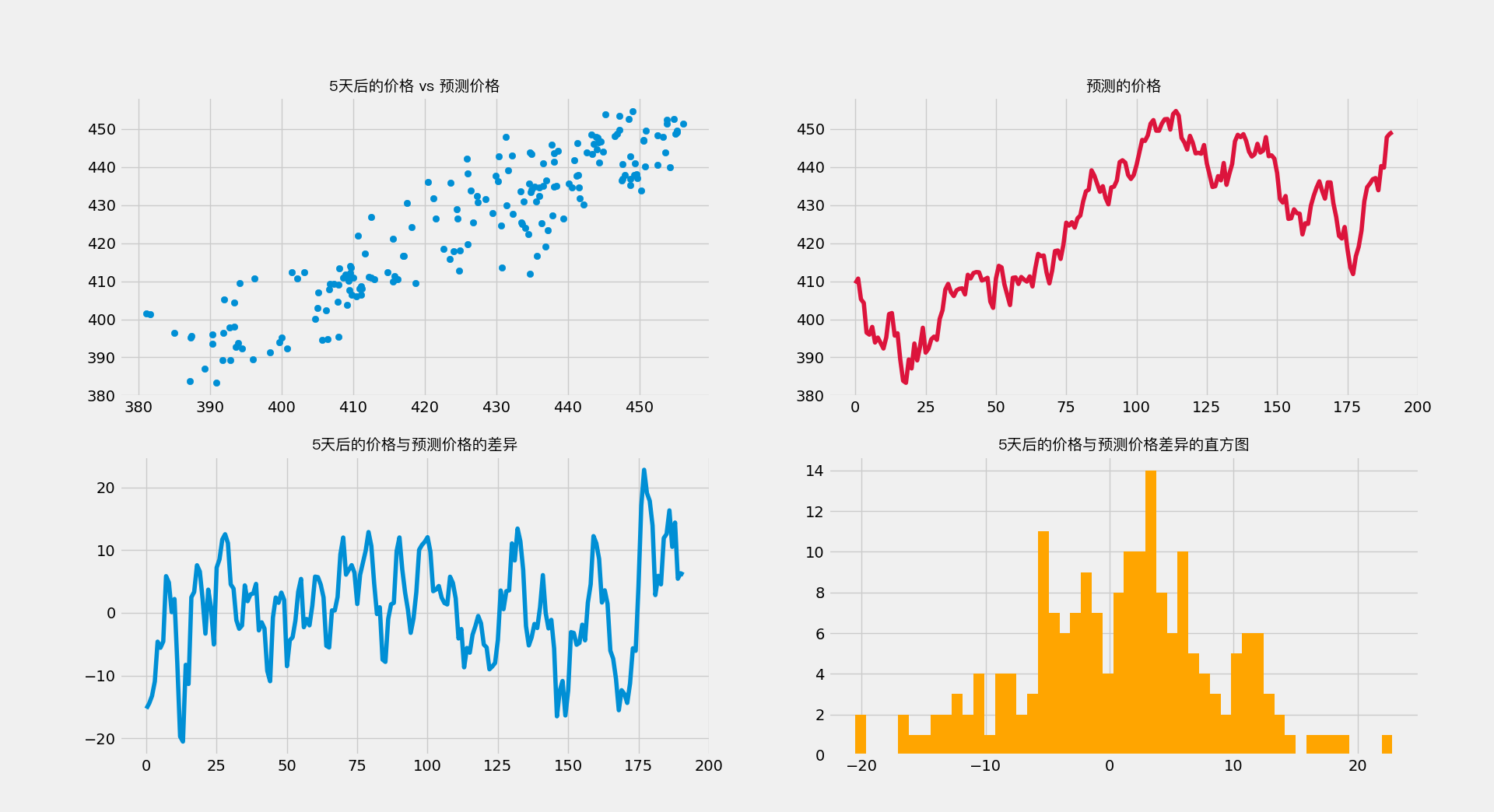
# 可视化预测结果和残差
fig, ax = plt.subplots(2, 2, figsize=(20, 10))

ax[0, 0].scatter(df3['X'], df3['y'])
ax[0, 0].set_title('5天后的价格 vs 预测价格', fontproperties=myFont)

ax[0, 1].plot(df3.index, y_pred[:-n], 'crimson')
ax[0, 1].set_title('预测的价格', fontproperties=myFont)

ax[1, 0].plot(df3.index, df3['X-y'])
ax[1, 0].set_title('5天后的价格与预测价格的差异', fontproperties=myFont)

ax[1, 1].hist(df3['X-y'], bins=50, density=False, color='orange')
ax[1, 1].set_title('5天后的价格与预测价格差异的直方图', fontproperties=myFont)

plt.show()

总结

支持向量机（SVM）的目标函数取决于处理的数据类型（线性可分、线性不可分、非线性）和相应的优化策略。以下是这三种情况下 SVM 的目标函数：

线性可分支持向量机（Hard Margin SVM）

对于线性可分的数据集，目标是找到一个最优的超平面，即最大化两个类别之间的间隔。

目标函数:$\min_{\mathbf{w}, b} \frac{1}{2} ||\mathbf{w}||^2$
约束条件: $y_i (\mathbf{w} \cdot \mathbf{x}_i + b) \geq 1, \quad \forall i$

线性不可分支持向量机（Soft Margin SVM）

当数据线性不可分时，通过引入“松弛变量”（slack variables）实现间隔和分类违规之间的平衡。

目标函数: $\min_{\mathbf{w}, b, \xi} \frac{1}{2} ||\mathbf{w}||^2 + C \sum_{i=1}^n \xi_i$
约束条件: $y_i (\mathbf{w} \cdot \mathbf{x}_i + b) \geq 1 - \xi_i, \quad \xi_i \geq 0, \quad \forall i$

非线性支持向量机

对于非线性数据集，目标函数和约束条件与线性不可分 SVM 类似，但使用核技巧在高维空间中寻找最优超平面。

目标函数: $\max_{\alpha} \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i,j=1}^n y_i y_j \alpha_i \alpha_j K(\mathbf{x}_i, \mathbf{x}_j)$
约束条件: $\sum_{i=1}^n y_i \alpha_i = 0 \text{ and } 0 \leq \alpha_i \leq C, \quad \forall i$ """

非线性 SVM 的优势与局限性

总结非线性 SVM 在处理复杂数据集时的优势，以及其面临的挑战和局限性。

往期推荐

欢迎扫码关注公众号，订阅更多文章!

欢迎扫