Devean 布洛克
K均值聚类(KMC) | 机器学习
November 13, 2023

K均值聚类(KMC) | 机器学习

发布 November 13, 2023  •  2 分钟  • 373 字
Table of contents

本文从概念、应用场景、原理、工作流程、优缺点、应用实践、代码、可视化等几方面诠释 K 均值聚类模型

概述

K-Means 是一种无监督的聚类算法，其目的是将 n 个数据点分为 k 个聚类。每个聚类都有一个质心，这些质心最小化了其内部数据点与质心之间的距离。

它能做什么

原理

初始化： 随机选择 k 个数据点作为初始聚类中心，这些可以是数据集中实际存在的点，也可以是随机生成的点。

分配： 遍历样本数据集，计算每个数据点到每个质心的距离，找出数据点距离最近的质心，将数据点分配给该聚类。

$d(p, q) = \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2 + \cdots + (p_n - q_n)^2}$

更新： 计算每个聚类内的平均值，并将平均值设为新的聚类中心。

假设我们有一个聚类 $C$，其中包含数据点 $ x_1, x_2, … x_n $，那么该集群的质心 $ \mu $ 可以使用以下公式计算：

$ \mu = \frac{1}{n} \sum_{i=1}^{n} x_i $

迭代： 重复分配和更新两步，直到质心不在显著移动或达到预定的迭代次数

优缺点

优点

缺点

选择正确的 K 值

局部最优解问题

处理不同大小和密度的集群

Python 实现

加载数据

import pandas as pd
from sklearn.datasets import load_iris

# 加载数据集
data = load_iris()
df = pd.DataFrame(data.data, columns=data.feature_names)

数据探索(EDA)

import seaborn as sns
import matplotlib.pyplot as plt

# 打印数据的头部和描述性统计
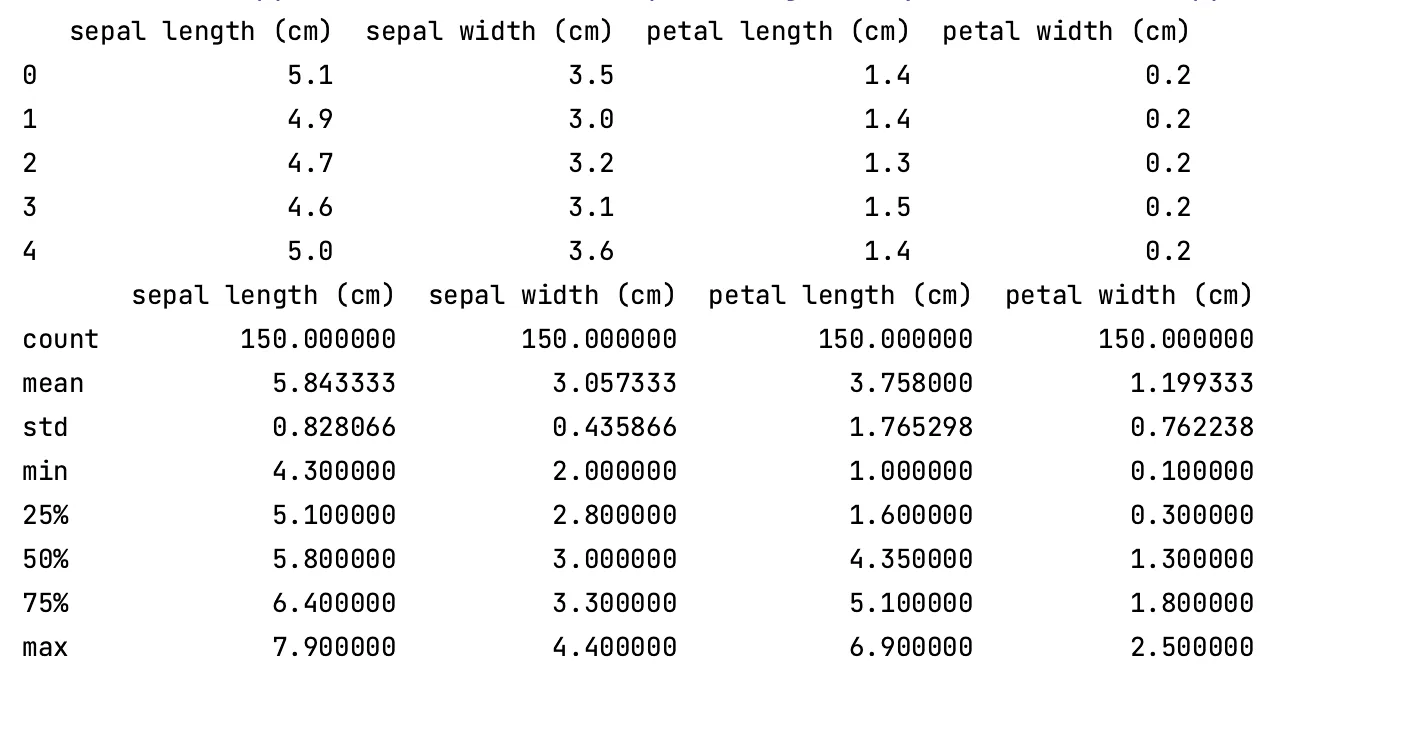
print(df.head())
print(df.describe())

# 使用pairplot查看数据的分布和特征间的关系
sns.pairplot(df)
plt.show()

# 检查数据中是否有缺失值
print(df.isnull().sum())

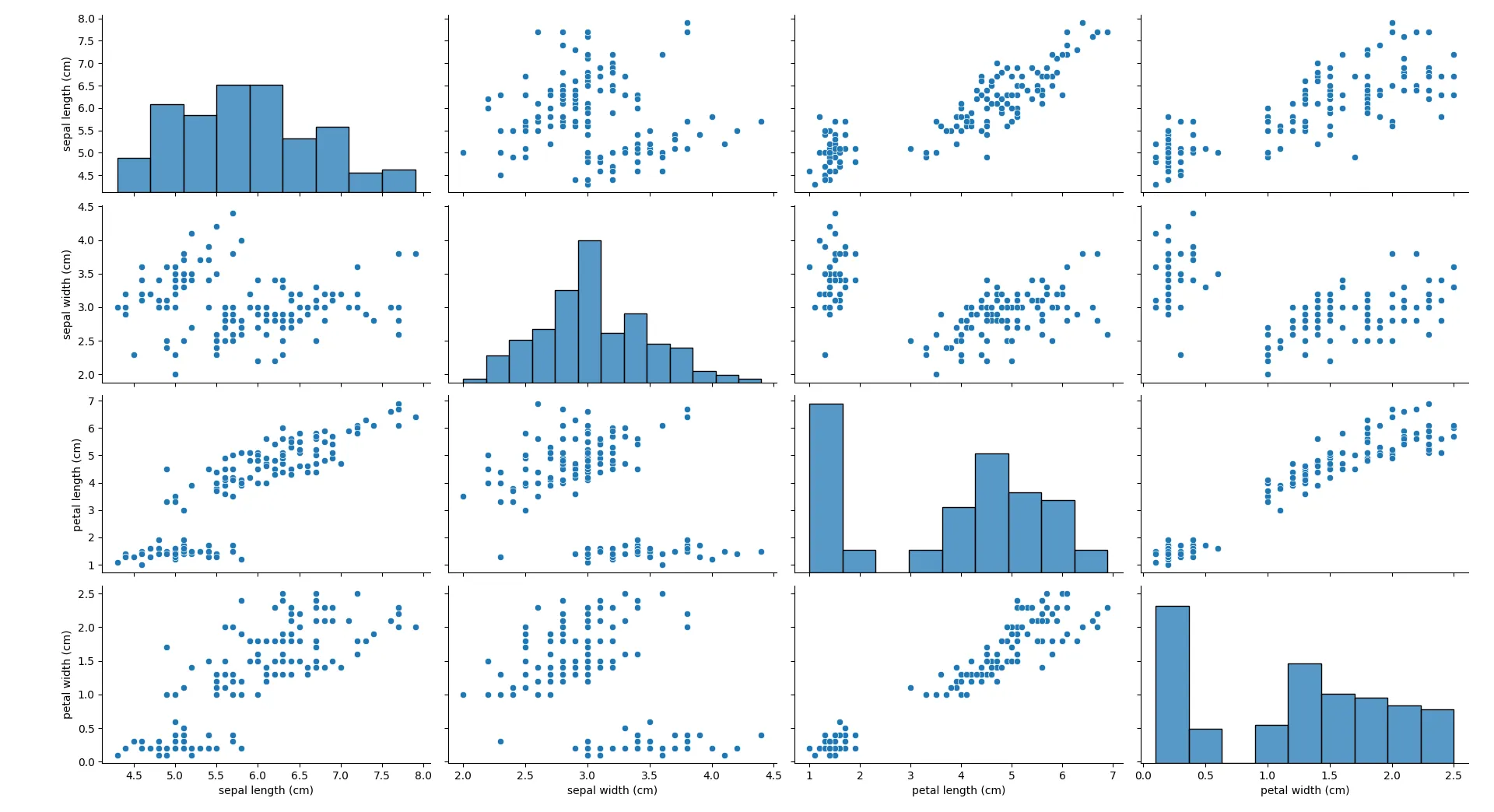
图中petal length和petal width之间存在明显的线性关系，并且可以看到至少两个明显的群集。具体的数值会因数据集而异，但可以观察到这些聚类的大致范围和关系。

数据预处理

from sklearn.preprocessing import StandardScaler

# 使用标准化器标准化数据（由于KMeans对特征的尺度敏感）
scaler = StandardScaler()
df_scaled = scaler.fit_transform(df)
df_scaled = pd.DataFrame(df_scaled, columns=df.columns)

特征工程

from sklearn.decomposition import PCA

# 使用PCA进行特征降维
pca = PCA(n_components=2)
data_2d = pca.fit_transform(df_scaled)
df_pca = pd.DataFrame(data_2d, columns=['PC1', 'PC2'])

模型训练

from sklearn.cluster import KMeans

# 进行K-Means聚类
kmeans = KMeans(n_clusters=3)
df_pca['cluster'] = kmeans.fit_predict(df_scaled)

可视化结果

# 使用散点图可视化PCA后的数据
plt.figure(figsize=(12, 6))
plt.scatter(df_pca['PC1'], df_pca['PC2'], c=df_pca['cluster'], cmap='viridis', s=50)
plt.title('PCA of Iris Dataset after K-Means Clustering')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.colorbar()
plt.show()

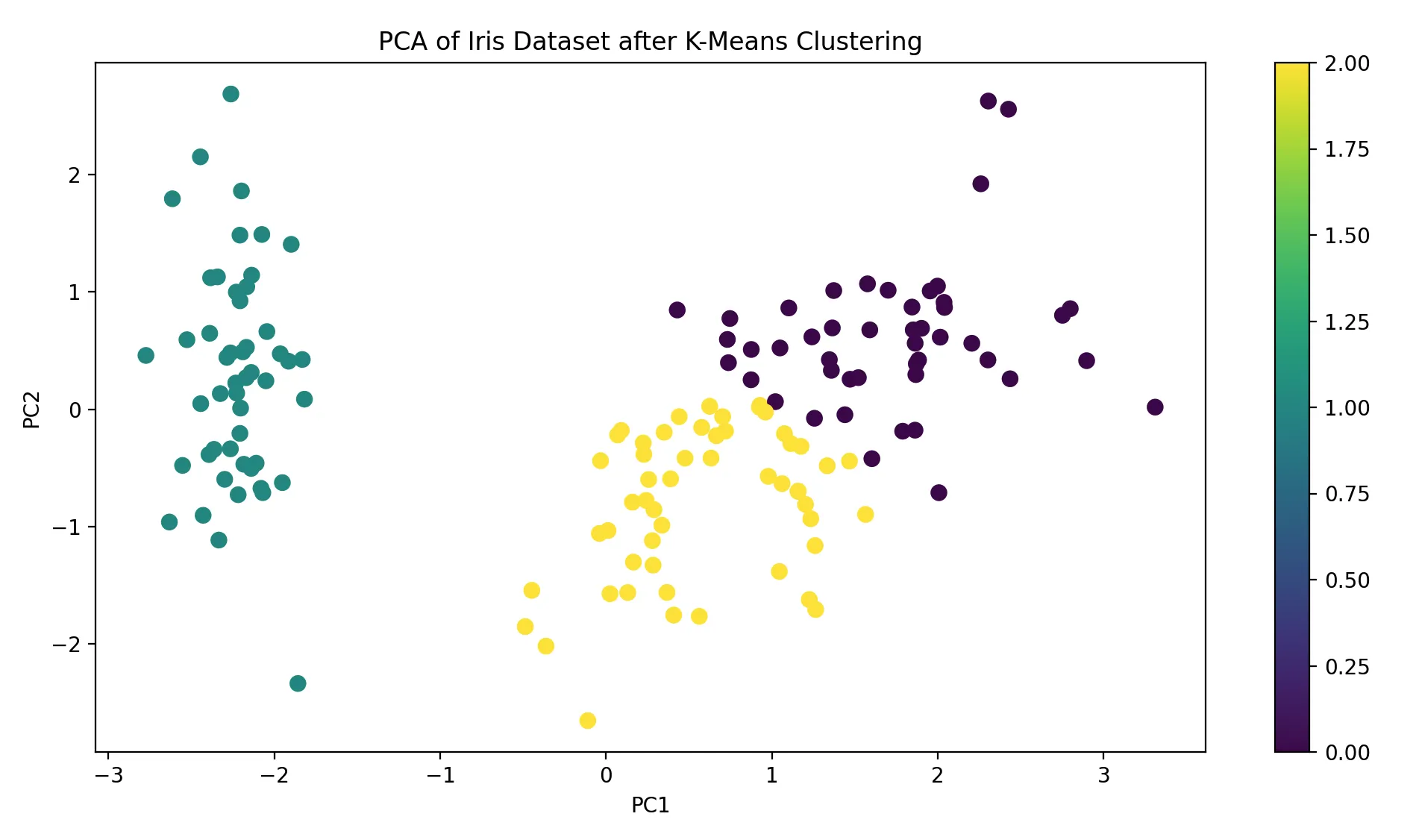
在此图中，你会看到三个明显的聚类（如果选择了k=3）。每个聚类的中心点可以通过查看KMeans的cluster_centers_属性来确定。这些中心点在PCA降维的2D空间中给出了聚类的中心位置。

# 使用并行坐标轴进行可视化
plt.figure(figsize=(12, 6))
pd.plotting.parallel_coordinates(df.assign(cluster=df_pca['cluster']), 'cluster', colormap='viridis')
plt.title('Parallel Coordinates Plot of Iris Dataset after K-Means Clustering')
plt.show()

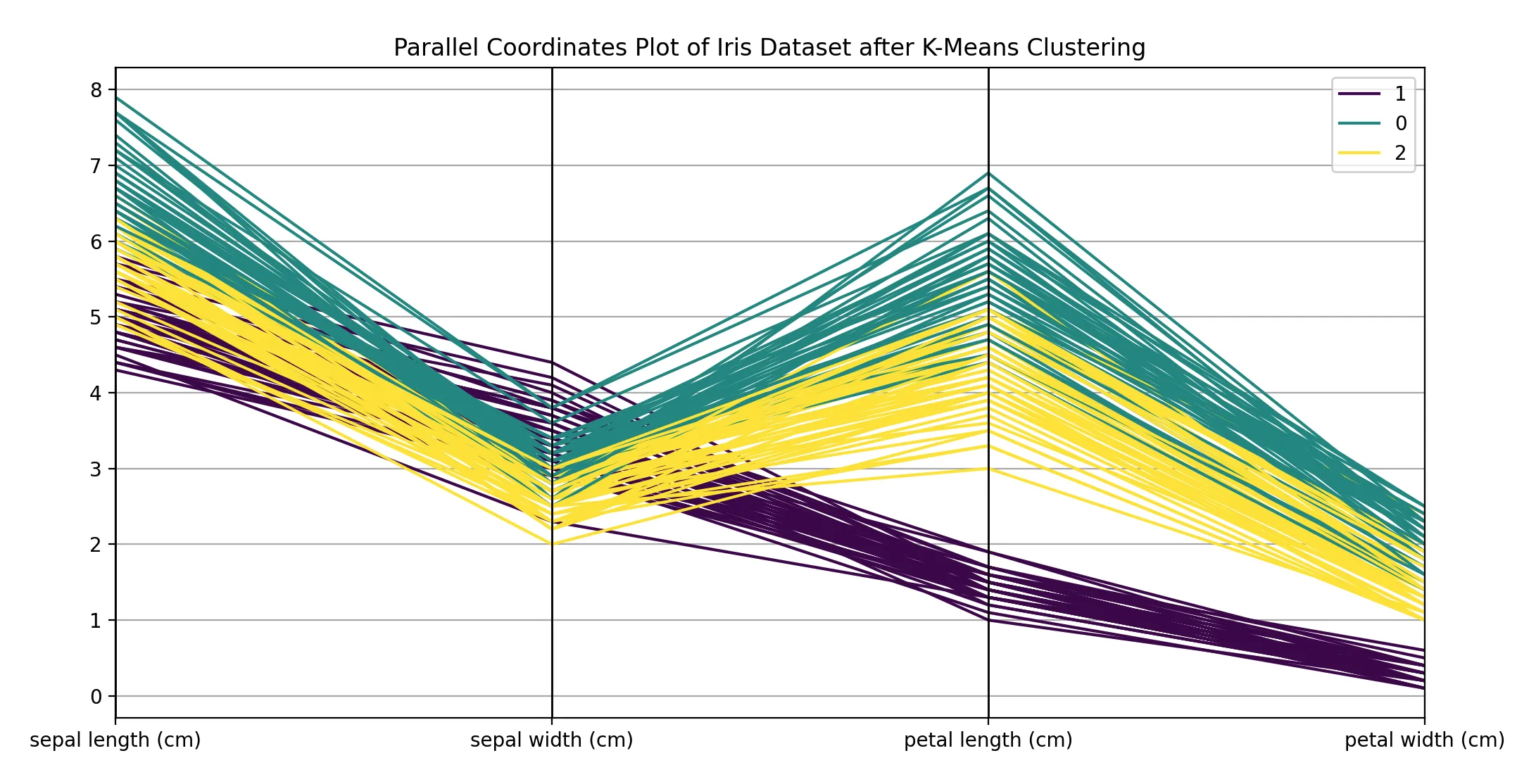
在此图中，你会注意到不同颜色的线表示不同的聚类。如果某个特征对于某个群集有显著的值，你会在该特征上看到这个群集的线与其他线有明显的分离。

模型评估

from sklearn.metrics import silhouette_score

# 计算不同K值的WCSS来选择最佳K值
wcss = []
k_values = range(1, 11)
for k in k_values:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(df_scaled)
    wcss.append(kmeans.inertia_)

plt.figure(figsize=(12, 6))
plt.plot(k_values, wcss, '-o')
plt.title('The Elbow Method')
plt.xlabel('Number of clusters (K)')
plt.ylabel('WCSS')
plt.show()

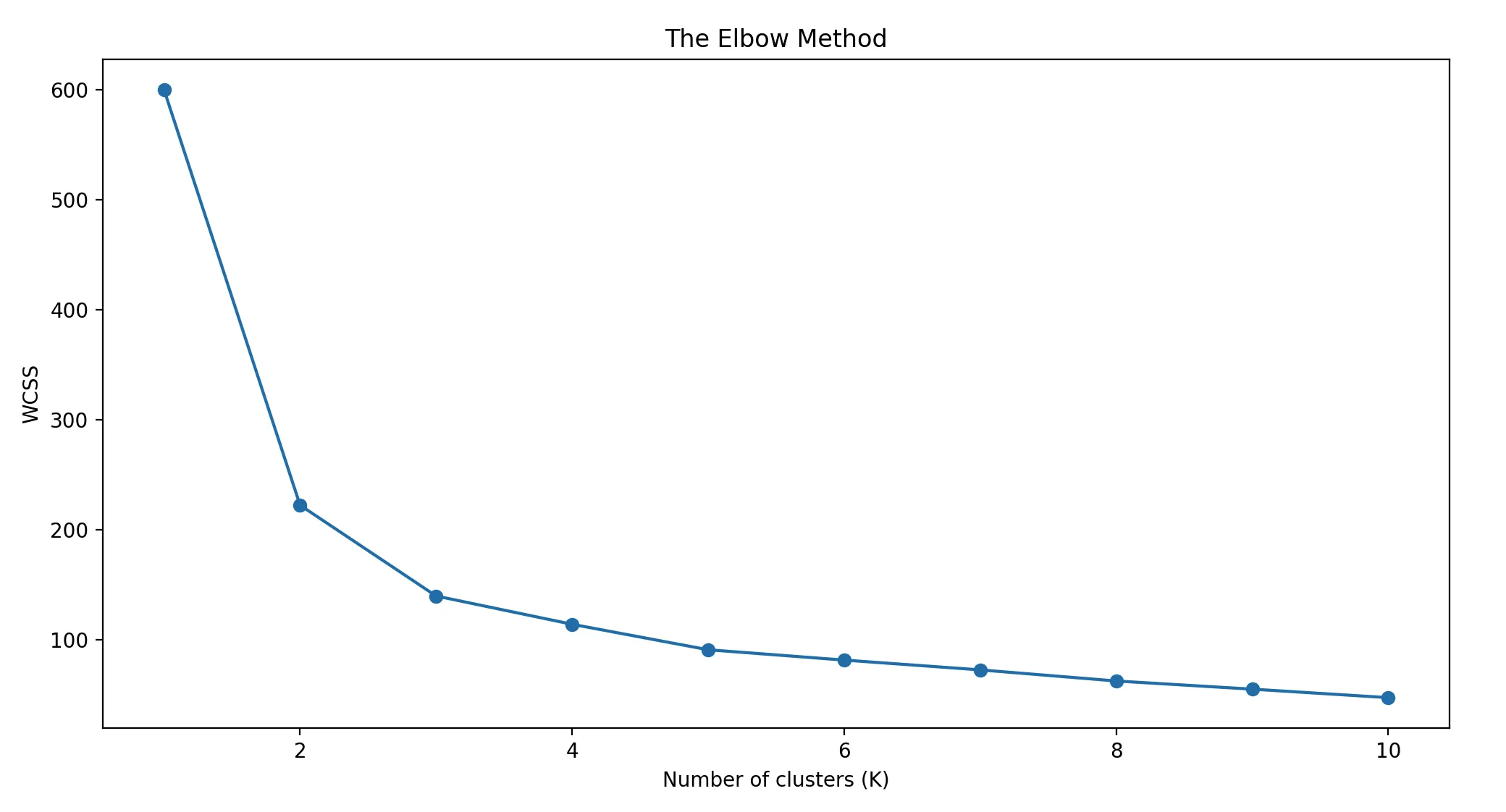
WCSS的值会随着K的增加而减少。在"肘点"，WCSS的下降速度会突然变慢。例如，如果在k=3时WCSS从400降到250，而在k=4时从250降到240，那么k=3可能是一个好的选择，因为增加更多的群集并没有显著降低WCSS。

# 使用轮廓系数评估聚类效果
k_values = range(2, 10)
silhouette_scores = []
for k in k_values:
    kmeans = KMeans(n_clusters=k, random_state=42).fit(df_scaled)
    labels = kmeans.labels_
    score = silhouette_score(df_scaled, labels)
    silhouette_scores.append(score)

plt.figure(figsize=(10, 6))
plt.plot(k_values, silhouette_scores, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Silhouette Score')
plt.title('Silhouette Score vs. Number of Clusters')
plt.grid(True)
plt.show()

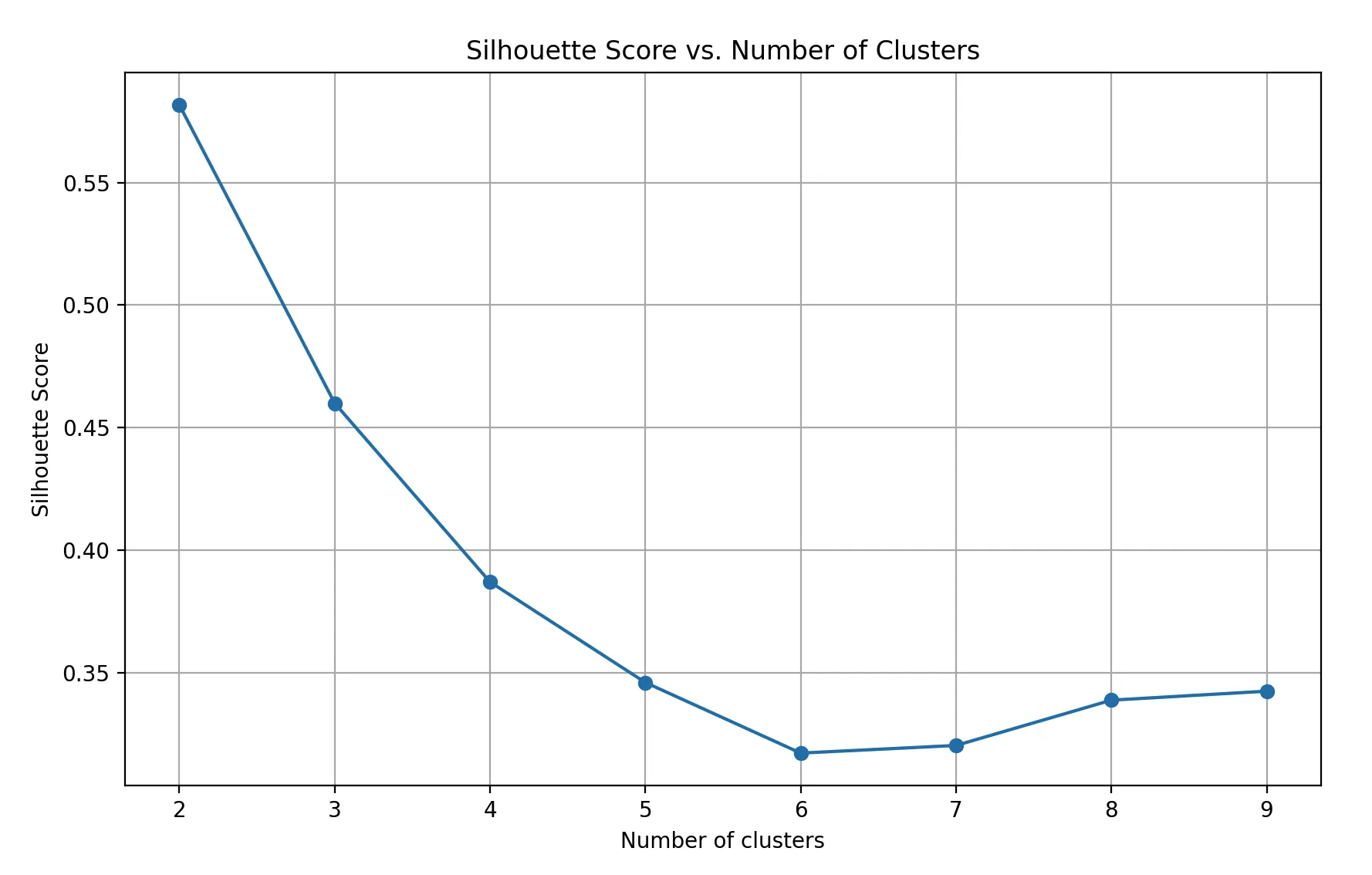
对于k=2到k=10的每个值，都会有一个轮廓系数。数值越接近1，表示聚类效果越好。你可以找到具有最高轮廓系数的k值。

# 显示每个群集的特征均值
cluster_means = df.assign(cluster=df_pca['cluster']).groupby('cluster').mean()

plt.figure(figsize=(10, 6))
sns.heatmap(cluster_means.T, cmap='coolwarm', annot=True)
plt.title('Feature Means by Cluster')
plt.show()

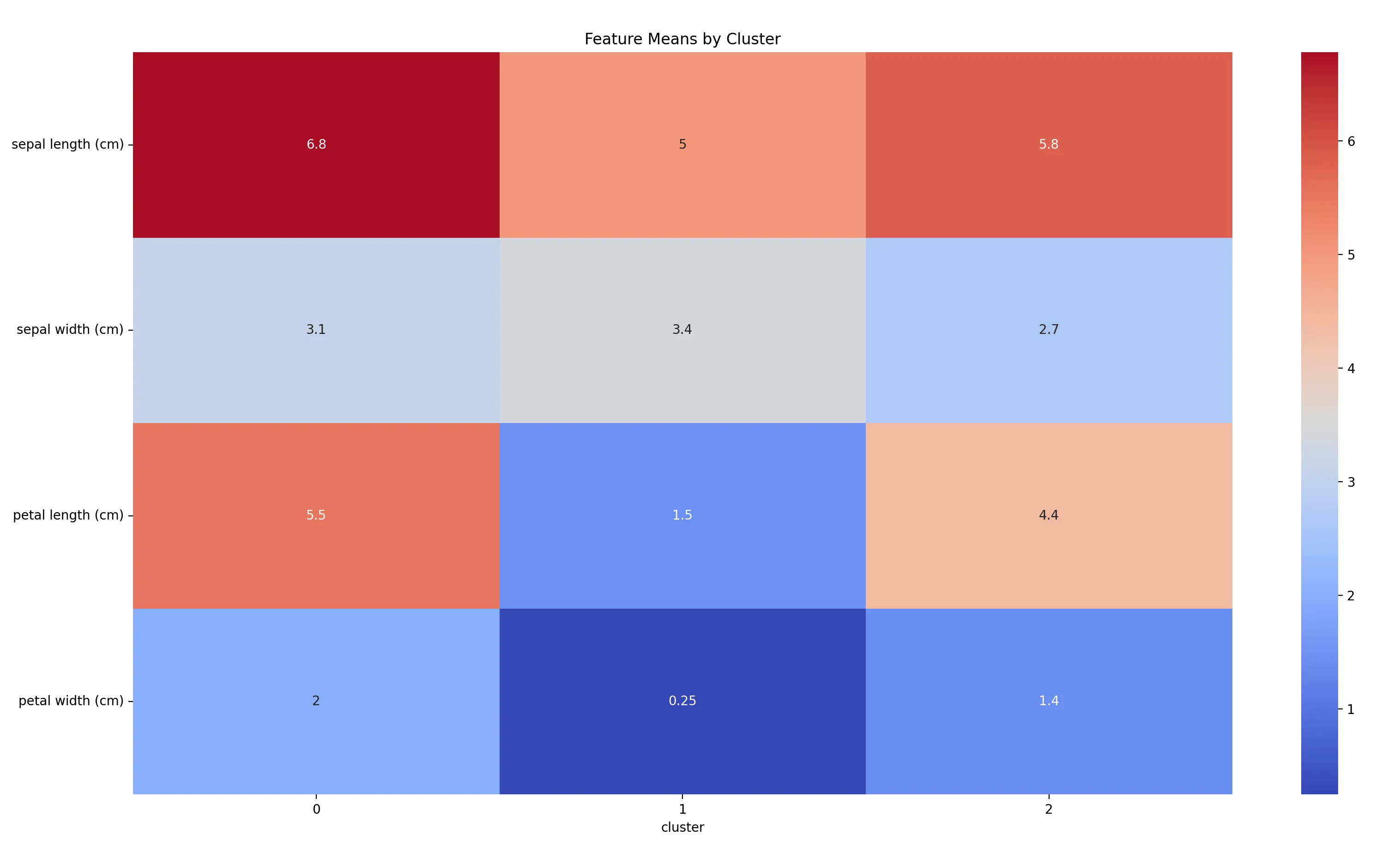
图中的数值显示了每个特征在每个群集中的平均值。例如，如果群集1的petal length均值为1.5，而群集2为4.4，那么这说明petal length是一个对于这两个群集有区分性的特征。

关注公众号每日思行发送:KMC代码 获取完整版源码

往期推荐